BOD - Das Digitale Betragsoptimum

Der Grundgedanke des Betragsoptimums, das ursprünglich für kontinuierliche Systeme hergeleitet wurde, ist näherungsfrei und in geschlossener Form für diskontinuierliche Systeme formulierbar. Damit kann bei betragsoptimaler Einstellung digitaler Regelkreise generell auf die Anwendung von Näherungsmethoden verzichtet werden:

*** Buch "Entwurf digitaler Regler für elektrische Antriebe"; Geitner, G.-H. ***
*** Aufsatz mit Grundgleichung und Beispielen: BOD_Zustand.pdf ***

Unter MATLAB steht eine Toolbox BOD mit m-Files sowie Demo's als Freeware bereit: aktuelle >>>Version 3.1<<<
bzw. ältere Versionen

Die Versionen unterscheiden sich in folgenden Punkten von Version 1.0:

• Wahlweise Ein- / Ausgabe von Übertragungsfunktionen in LTI-Syntax.
• Wahlweise vektorgesteuerte Optimierung mit wahlweiser Abschaltung von Rückmeldungen.
• Überarbeitete Berechnung von Kaskadenstrukturen. Bei Anpassung an die Syntax können neben Endlicher Einstellzeit und Digitalem Betragsoptimum auch andere Optimierungsverfahren verwendet werden.
• Wesentlich erweiterte Demo's mit SIMULINK Simulation.
• Einführung von private- und DEMO-Direktory sowie content File.
• V.2.3: Einführung Englischer Hilfetexte (help).
• V.2.4: Die neue Funktion "bod_gen.m" verwendet generell direkt das BOD Grundgleichungssystem zur Optimierung, um Regler der PID-Familie, verwandte Regler und Lead/Lag Regler zu berechnen. Hierin besteht ein wesentlicher Unterschied zur Funktion "bod.m" die auf Umformungen des BOD Grundgleichungssystems basiert.
• V.2.5: Die neue Funktion "gmt.m" erlaubt die Berechnung von gewichteten mittleren Totzeiten bei Einsatz von Bussystemen innerhalb der Regelschleife; Die Unterdirektorie "SYMDEF" ermöglicht die symbolische Definition von Regler und Strecke, mehrere Beispiele mit Definitionen und Simulink-Modellen veranschaulichen die Anwendung.
• V.2.8: Anpassung an veränderte Syntax für fsolve
• V.2.9: nargchk entfällt zukünftig, Ersatz durch narginchk
• V.3.0: Neue Funktion "bod_rst.m" mit Beispiel "demo_BOD_rst.m"
• V.3.1: Neue Funktion "bod_prefi_opt.m" mit Beispielen "bod_prefi_opt_check01_..." bis "bod_prefi_opt_check05_..." zur hybriden Optimierung, d.h. Reglereinstellung bewirkt Verhalten für verzögerte Eingangsgrößen, Einstellung des Vorfilters bewirkt Verhalten für unverzögerte Eingangsgrößen

Allgemeine Vorteile des Betragsoptimums - bereits verfügbar für kontinuierliche Systeme:

• Geringe Stellgliedbeanspruchung
• Relativ geringe Parameterempfindlichkeit
• Einfache Regler- und Parameterberechnungsgleichungen
• Einfache Modelle für unterlagerte, geschlossenen Regelkreise sind praktikabel
• Relativ geringer Unterschied im Führungsverhalten zwischen unverzögerten und verzögerten Eingangssignalen mit vorgeschaltetem Filter
• Zielt auf geeignete Formung des anschaulichen Zeitverhaltens - damit praktisch interessanter als z.B. Polvorgabe
• Anwendbar auf Zustandsregelungen durch Berechnung über Ausgangsgleichungssystem

Weitere Vorteile des Digitalen Betragsoptimums (BOD) zur Berechnung diskontinuierlicher Regler:

• Einsetzbar für beliebige Relationen zwischen Abtastzeit und Streckenzeitkonstante
• Einfache Berücksichtigung von ganzzahligen und nichtganzzahligen Totzeiten
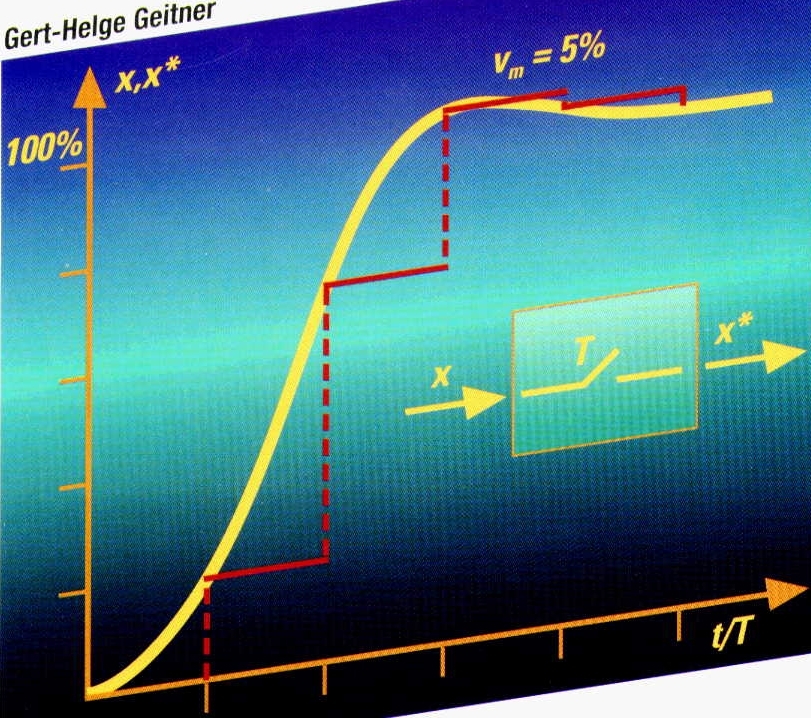
• Einfache und genaue Berücksichtigung von Mittelwertmessungen
• Einfache Berücksichtigung von Stellgliedmodellen auf Abtasterbasis
• Keine Notwendigkeit zur Definition einer Summenzeitkonstante bzw. zur Nichtkompensation der kleinsten Zeitkonstante, um einfache Ergebnisse zu erhalten
• In bestimmten Fällen für nichtminimalphasige Strecken einsetzbar
• Eine Verstärkungsreduktion auf 2/3 erweist sich meist als günstiger Anfangswert für eine aperiodische Einstellung bei unverzögerten Eingangsgrößen
• Übersichtliche Berechnung von Zustandsregelstrukturen
• Direkter Entwurf digitaler Regler ausgehend von leistungsflussorientierten Streckenmodellen

Wie für kontinuierliche Systeme gilt:

• Einsetzbar für Kaskaden- und Zustandsregelstrukturen
• Anwendbar bei unverzögerten und verzögerten Eingangssignalen, d.h. das sogenannte Symmetrische Optimum ist eingeschlossen.
• Typische Reglerstrukturen bei Kaskadenstruktur sind: P-, I-, PI-, PD-, PID-Regler
• Eine Kompensation von Streckenpolen kann bei Bedarf erfolgen

Die Ergebnisse sind sowohl für maschinelle Berechnungen, als auch für Berechnungen von Hand bzw. on-line Adaption aufbereitet - siehe Literaturstelle. Maschinelle Berechnung der Reglerparameter und Z-Transformation der Strecke erfolgen günstig mit einem Mathematikprogramm-Paket wie z.B. MATLAB .