BOD - The Digital Magnitude Optimum

The Magnitude Optimum was deduced for continuous systems originally. The basic idea is to achieve as large frequency range of closed loop gain identically to unity as possible. This aim may be mathematically defined for discontinuous systems likewise avoiding any approximation and defining a closed formula. Thus the use of the Digital Magnitude Optimum generally makes it possible to avoid quasicontinuous methods for optimization of discontinuous control loops based on the Magnitude Optimum:

*** Book "Design of digital controllers for electric drives" (in German); Geitner, G.-H. ***
*** Paper containing the basic equation system and examples: BOD_Eng.doc.Z ***

Applying MATLAB - freeware toolbox BOD is at disposal containing m-files and demo's: current >>>Version 3.1<<<

The versions differ in following features to version 1.0:

• Optionally use of LTI syntax to input / output transfer functions instead of numerator / denominator polynomials.
• Optionally control vector-driven optimization instead of menu-driven operation and optionally switch-off of messages.
• Revision of cascaded control structure computations. In addition to Digital Magnitude Optimum and Finite Time Settling another optimization rules may be applied if syntax is matched to.
• More comprehensive demo's including Simulink simulations.
• Introduction of directories "private" and "demo" as well as of a content file.
• V.2.3: complete English help.
• V.2.4: New function "bod_gen.m" generally applies the basic BOD optimization equation system directly to compute PID-type family, similar and lead / lag controllers. This is an essential contrast to function "bod.m" which is based on reconfigurations of the BOD optimization equation system.
• V.2.5: New function "gmt.m" enables computation of weighted mean dead times in case of application of bus systems within control loops; subdirectory "SYMDEF" offers symbolic definition of controller and plant, several examples examplify application via definitions and Simulink models.
• V.2.8: tuning for modified fsolve syntax
• V.2.9: nargchk obsolete, replaced by narginchk
• V.3.0: new function "bod_rst.m" and example "demo_BOD_rst.m"
• V.3.1: new function "bod_prefi_opt.m" with examples "bod_prefi_opt_check01_..." till "bod_prefi_opt_check05_..." for hybrid optimization, i.e. controller settings cause behaviour for delayed inputs, settings of prefilter cause behaviour for undelayed inputs

General advantages of the Magnitude Optimum - already available for continuous systems:

• Low stress of the electric actuator
• Relatively low parameter sensitivity
• Easy equations to calculate the parameters of the controller
• Feasible easy models of inner closed control loops
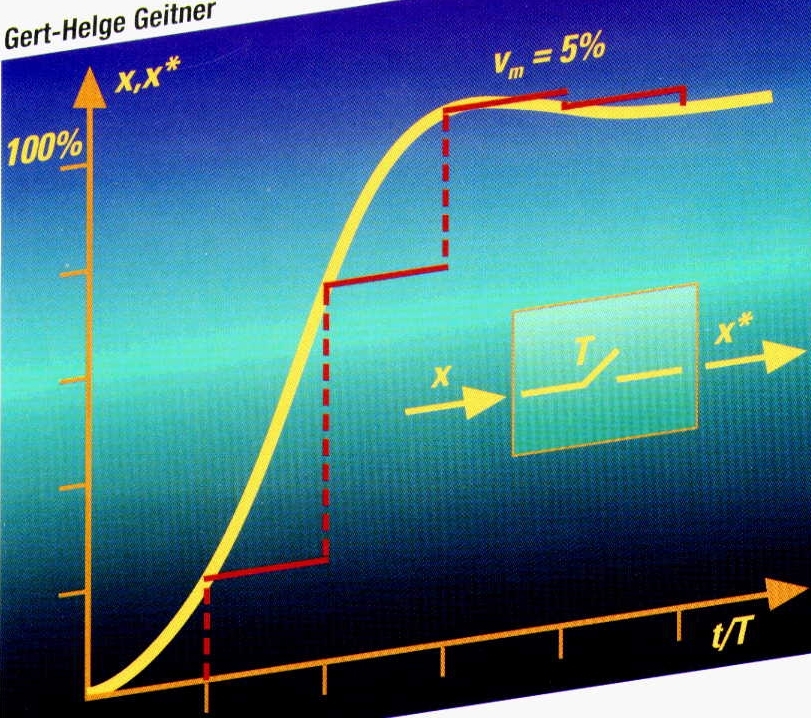
• Little difference only between the step response behaviour regarding undelayed signals and delayed input signals including pre-filters
• Aimed to an influence on the clear time behaviour, therefore practically more interesting in comparison to pole placement
• Applicably for state control structures via use of the basic equation system

More general advantages only available applying the Digital Magnitude Optimum for discontinuous systems:

• Valid regarding any relation of sampling time and time constants of the controlled process
• Easy consideration of whole-number and not whole-number dead times regarding structure and dimensioning of the controller
• Easy consideration of mean value measurements of controlled variables without any approximation
• Easy consideration of models of actuators based on samplers regarding the innermost loop
• Not any longer the need for a definition of a sum of the parasitic time constants resp. for a non-compensation of the smallest time constant to get easy results
• Practicable on not minimal-phase systems in particular cases
• Gain reduction to 2/3 proves to be a successful starting point for an aperiodic adjustment regarding undelayed input signals in particular cases
• Calculation of the intended delay of a derivative component in particular cases
• Direct digital control design based on power flow oriented plant models

As valid for continuous systems it is valid for discontinuous systems likewise:

• Applicable for cascaded and state control structures.
• Applicable for undelayed and delayed input signals, latter with pre-filter, thus the so-called symmetrical optimum is included.
• All typical controller types of the PID-family are included: P, I, PI, PD, PID.
• Compensation of stable poles is possible if desired.

The results of the Digital Magnitude Optimum are prepared as well as for computer-aided and manual use - see book above. The latter reconfigurations are an important base for on-line adaptation algorithms also. Computer-aided computations of z-transformed plants and controller parameters advantageously may be executed via mathematical software packages like MATLAB, for instance using above mentioned toolbox BOD.