- Adrian Lange, Christian Gollwitzer, Robert Maretzki, Ingo Rehberg and Reinhard Richter
"Retarding the growth of the Rosensweig instability unveils a new scaling regime" in
Phys. Rev. E 93, (2016) 034106
- Thomas Friedrich, Adrian Lange, Ingo Rehberg, and Reinhard Richter
"A note on the magnetic spatial forcing of a ferrofluid layer" in
Magnetohydrodynamics 47, (2011) 167
- Reinhard Richter and Adrian Lange
"Surface instabilites of ferrofluids" in
Lecture Notes of Physics 763, Ed. S. Odenbach, Springer-Verlag, Berlin, (2009) 157
- Holger Knieling, Adrian Lange, Gunar Matthies, Ingo Rehberg, and Reinhard Richter
"Maximal growth rate at the Rosensweig instability: theory, experiment, and numerics" in
Proc. Appl. Math. Mech. 7 (2007) 4140025
- Holger Knieling, Reinhard Richter, Ingo Rehberg, Gunar Matthies, and Adrian Lange
"Growth of surface undulations at the Rosensweig instability" in
Phys. Rev. E 76 (2007) 066301
- Adrian Lange, Reinhard Richter, and Lutz Tobiska
"Linear and nonlinear approach to the Rosensweig instability" in
GAMM Mitt. 30 (2007) 171
- V. V. Mekhonoshin and Adrian Lange
"Chain-induced effects in the Faraday instability on ferrofluids in a horizontal magnetic field" in
Phys. Fluids 16 (2004) 925
- Adrian Lange
"Instabilitäten magnetischer Flüssigkeiten in statischen Magnetfeldern",
habilitation thesis (2003)
- Bert Reimann, Reinhard Richter, Ingo Rehberg, and Adrian Lange
"Oscillatory decay at the Rosensweig instability: experiment and theory" in
Phys. Rev. E 68 (2003) 036220
- Reinhard Richter, Bert Reimann, Adrian Lange, Peter Rupp, and Alexander Rothert
"Magnetic Liquid Patterns in Space and Time" in
Advances in Solid State Physics 43 (2003) 789
- Adrian Lange
"Decay of metastable patterns for the Rosensweig instability: revisiting the dispersion relation" in
Magnetohydrodynamics 39 (2003) 65
- V. V. Mekhonoshin and Adrian Lange
"Faraday instability on viscous ferrofluids in a horizontal magnetic field: Oblique rolls of arbitrary orientation" in
Phys. Rev. E 65 (2002) 061509
- Adrian Lange
"The Adjoint Problem in the Presence of a Deformed Surface: the Example of the Rosensweig Instability on Magnetic Fluids" in
Int. J. Modern Phys. B 16 (2002) 1155
- Adrian Lange
"Kelvin force in a Layer of Magnetic Fluid" in
J. Magn. Magn. Mat. 241 (2002) 327
- Adrian Lange, Bert Reimann, and Reinhard Richter
"Wave number of maximal growth in viscous ferrofluids" in
Magnetohydrodynamics 37 (2001) 261
- Adrian Lange
"Scaling Behaviour of the Maximal Growth Rate in the Rosensweig Instability" in
Europhys. Lett. 55 (2001) 327
- Adrian Lange, Bert Reimann, and Reinhard Richter
"Wave Number of Maximal Growth in Viscous Magnetic Fluids" in
Proceedings 4th Pamir International Conference, Presqu'ile de Giens Sept. 2000
- Adrian Lange, Bert Reimann, and Reinhard Richter
"Wave Number of Maximal Growth in Viscous Magnetic Fluids of Arbitrary Depth" in
Phys. Rev. E 61 (2000) 5528
- Adrian Lange, Heinz Langer, and Andreas Engel
"Dynamics of a Single Peak of the Rosensweig Instability in a Magnetic Fluid" in
Physica D 140 (2000) 294
- A. Engel, A. Lange, H. Langer, T. Mahr, and M. V. Chetverikov
"A single peak of the Rosensweig instability" in
J. Magn. Magn. Mat. 201 (1999) 310
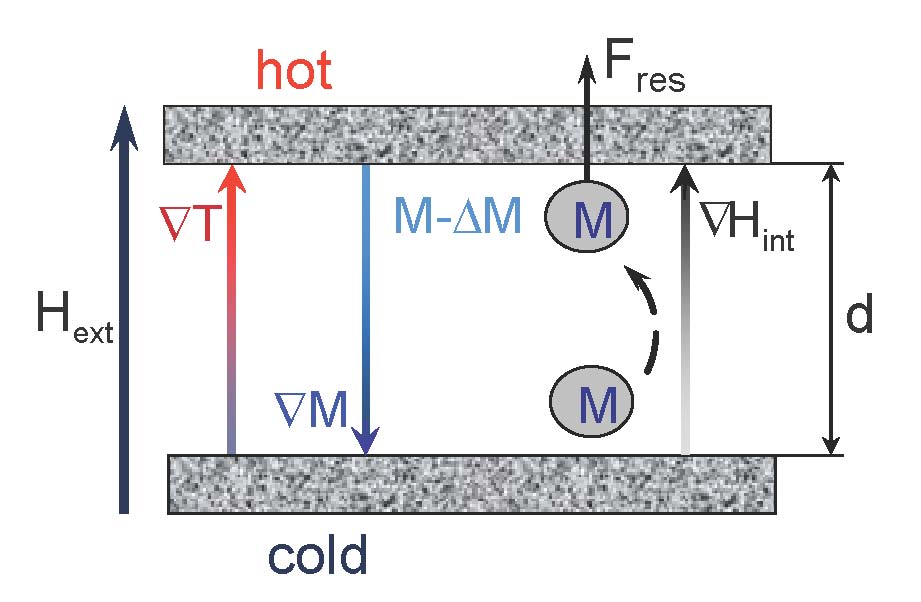 To describe the appearance of the thermomagnetic convection
a horizontal layer of magnetic fluid between two rigid boundary plates is considered. The lower one
is cooled, the upper one is heated. Additionally an external magnetic field Hext
oriented vertically
is applied. Due to the temperature gradient ∇T in the fluid layer, the magnetization of the magnetic fluid
shows a gradient ∇M pointing in opposite direction as ∇T. The gradient in the magnetization
causes now another gradient, that of the internal magnetic field, ∇Hint,
which is antiparallel to ∇M. If a fluid element with the magnetization M from the bottom
is moved adiabatically
to the top of the layer, where the magnetization M-ΔM prevails, a resulting force
To describe the appearance of the thermomagnetic convection
a horizontal layer of magnetic fluid between two rigid boundary plates is considered. The lower one
is cooled, the upper one is heated. Additionally an external magnetic field Hext
oriented vertically
is applied. Due to the temperature gradient ∇T in the fluid layer, the magnetization of the magnetic fluid
shows a gradient ∇M pointing in opposite direction as ∇T. The gradient in the magnetization
causes now another gradient, that of the internal magnetic field, ∇Hint,
which is antiparallel to ∇M. If a fluid element with the magnetization M from the bottom
is moved adiabatically
to the top of the layer, where the magnetization M-ΔM prevails, a resulting force
Fres=M ∇Hint - (M-ΔM) ∇Hint = + ΔM ∇Hint
is generated. This force has the same positive z-direction as the adiabatic movement.
Thus initial disturbances will be enhanced and can lead to the onset of thermomagnetic convection
if the stabilizing effects of heat conduction and internal friction can be overcome. This type of
heat and mass transfer was first theoretically analyzed by Finlayson [1] and later on experimentally
studied by Schwab [2-3] for the very first time.
[1] B. A. Finlayson, J. Fluid Mech. 40, 753 (1970).
[2] L. Schwab and K. Stierstadt, J. Magn. Magn. Mat. 65, 315 (1987).
[3] L. Schwab, J. Magn. Magn. Mat. 85, 199 (1990).




 Surface instabilities of magnetic fluids
Surface instabilities of magnetic fluids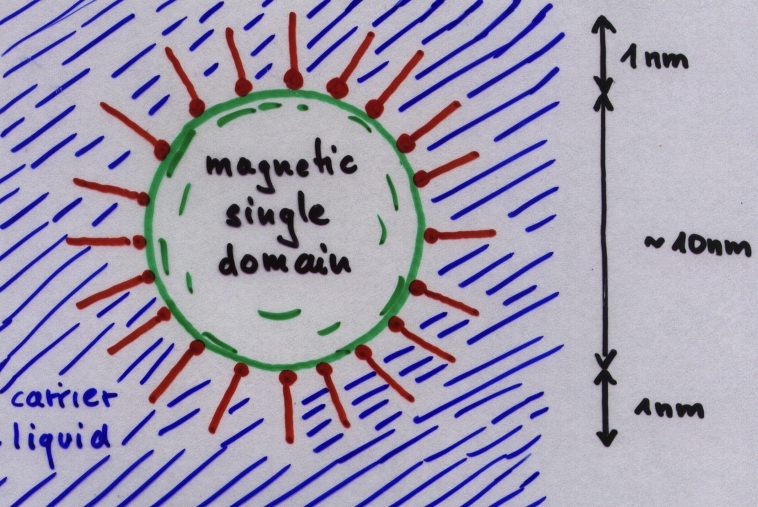 Magnetic fluids are stable colloidal suspensions
of ferromagnetic nanoparticles (typically magnetite or cobalt) dispersed in
a carrier liquid (typically oil or water). The nanoparticles are coated with
a layer of chemically adsorbed surfactants to avoid agglomeration. Magnetic
fluids are
Magnetic fluids are stable colloidal suspensions
of ferromagnetic nanoparticles (typically magnetite or cobalt) dispersed in
a carrier liquid (typically oil or water). The nanoparticles are coated with
a layer of chemically adsorbed surfactants to avoid agglomeration. Magnetic
fluids are Thermomagnetic convection in magnetic fluids
Thermomagnetic convection in magnetic fluids To describe the appearance of the thermomagnetic convection
a horizontal layer of magnetic fluid between two rigid boundary plates is considered. The lower one
is cooled, the upper one is heated. Additionally an external magnetic field Hext
oriented vertically
is applied. Due to the temperature gradient ∇T in the fluid layer, the magnetization of the magnetic fluid
shows a gradient ∇M pointing in opposite direction as ∇T. The gradient in the magnetization
causes now another gradient, that of the internal magnetic field, ∇Hint,
which is antiparallel to ∇M. If a fluid element with the magnetization M from the bottom
is moved adiabatically
to the top of the layer, where the magnetization M-ΔM prevails, a resulting force
To describe the appearance of the thermomagnetic convection
a horizontal layer of magnetic fluid between two rigid boundary plates is considered. The lower one
is cooled, the upper one is heated. Additionally an external magnetic field Hext
oriented vertically
is applied. Due to the temperature gradient ∇T in the fluid layer, the magnetization of the magnetic fluid
shows a gradient ∇M pointing in opposite direction as ∇T. The gradient in the magnetization
causes now another gradient, that of the internal magnetic field, ∇Hint,
which is antiparallel to ∇M. If a fluid element with the magnetization M from the bottom
is moved adiabatically
to the top of the layer, where the magnetization M-ΔM prevails, a resulting force Flow dynamics and stability of the density oscillator
Flow dynamics and stability of the density oscillator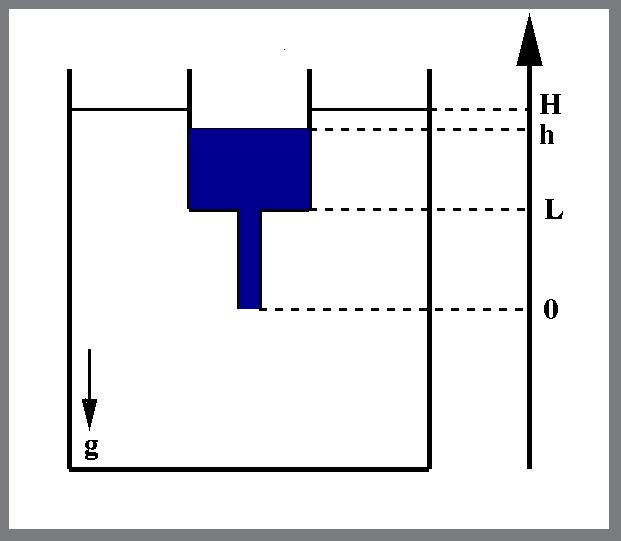

 Pattern formation in water-sand mixtures
Pattern formation in water-sand mixtures

 Electrohydrodynamic convection in liquid crystals and multiplicative noise
Electrohydrodynamic convection in liquid crystals and multiplicative noise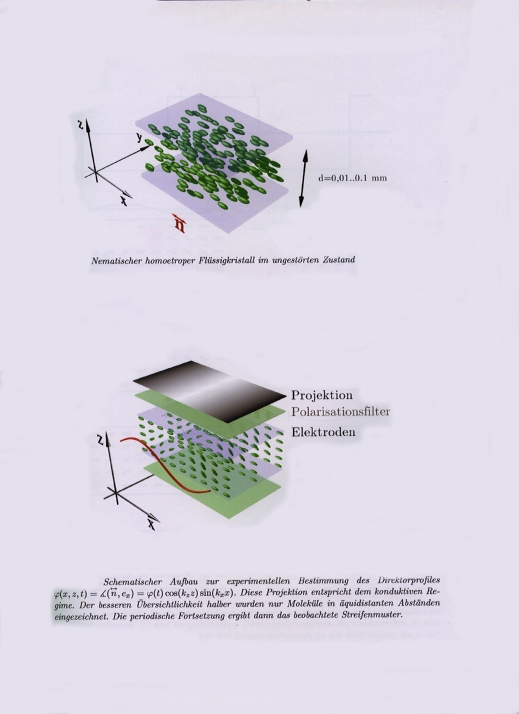
 Personal homepage
Personal homepage