Übung zur Nutzung von MS-Excel
Grundlagen
Hier finden Sie Ausführungen zu Grundlagen der Arbeit mit MS-Excel
Teil 1
Diagramme
Stellen Sie folgende Messwerte
|
Zeit in min |
Wasserstand in m |
|
0 |
14,0 |
|
1 |
14,5 |
|
2 |
14,7 |
|
4 |
14,9 |
|
10 |
15,0 |
mittels MS-Graph (Diagrammfunktion im MS-Excel) grafisch dar.
Hier finden Sie die Arbeitsschritte zur Erstellung von Diagrammen
Hier finden Sie die Lösungs-MS-Excel-Datei
zum Teil 1
Teil 2
Berechnen Sie für verschiedene Wurfparabeln die
zugehörigen Eigenschaften (Höhe h, Weg s, Geschwindigkeit v) in Abhängigkeit
von der Zeit t (0 bis 10 s) und stellen Sie die Beziehungen grafisch dar. Die
Erdbeschleunigung g beträgt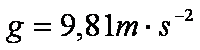
.
Benutzen Sie bei der grafischen Darstellung die Anfangsgeschwindigkeiten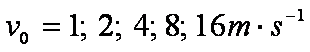 
als Parameter.
1. Waagerechter
Wurf
Die Wurfhöhe in Abhängigkeit von der Zeit wird nach
folgender Formel berechnet: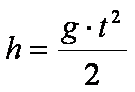 
die Wurfweite nach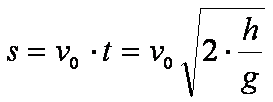 
die Wurfgeschwindigkeit nach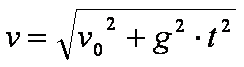 
2. Schiefer
Wurf
Die Wurfhöhe in
Abhängigkeit von der Zeit wird nach folgender Formel berechnet: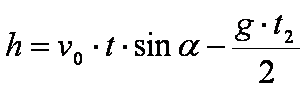 
die Wurfweite nach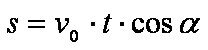 
die maximal erreichbare Wurfweite nach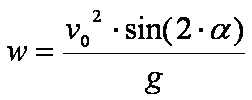 
die Wurfgeschwindigkeit nach 
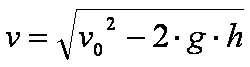
Der Wurfwinkel a soll als Parameter dienen. Verwenden Sie
für a
Werte zwischen 0 und 900 mit einer Stufung von 50.
Hier finden Sie die Arbeitsschritte zur Berechnung der Wurfparabeln
Hier finden Sie die Lösung zu Teil 2
Teil 3
Das Übertragungsverhalten für Verzögerungssysteme
1. Ordnung kann durch folgende Gleichung beschrieben werden:
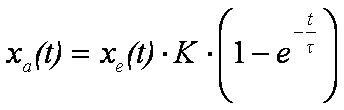
A. Der
Absenkungsverlauf des Grundwassers auf Grund einer Entnahme aus einem Brunnen
(z.B. durch einen so genannten. Pumpversuch) kann in erster Näherung durch
solch eine Funktion ersetzt werden. Dabei bezeichnet K die hydraulische
Leitfähigkeit des Grundwasserleiters.
Für das Produkt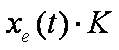 
soll der Wert 1,24
eingesetzt werden. Die Zeit, bei der die Absenkung den Wert von 
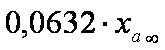erreicht hat, wird mit t bezeichnet. Dabei bezeichnet xa¥
die maximale Absenkung.
1. Stellen Sie den Absenkungsverlauf aus den Werten des Pumpversuches (siehe Vorlage in einem Diagramm dar.
2. Bestimmen Sie aus dem Diagramm die Werte für t und xa¥
3. Berechnen Sie die Absenkungskurve nach der oben genannten Übertragungsfunktion.
4. Berechnen Sie die quadratische Abweichung zwischen den gemessenen und den berechneten Werten und stellen Sie beide grafisch dar.
B. Exakterweise
kann die Absenkung s eines Brunnens mittels der Theis-Funktion berechnet werden. 
bezeichnet dabei die
so genannte Brunnenfunktion.
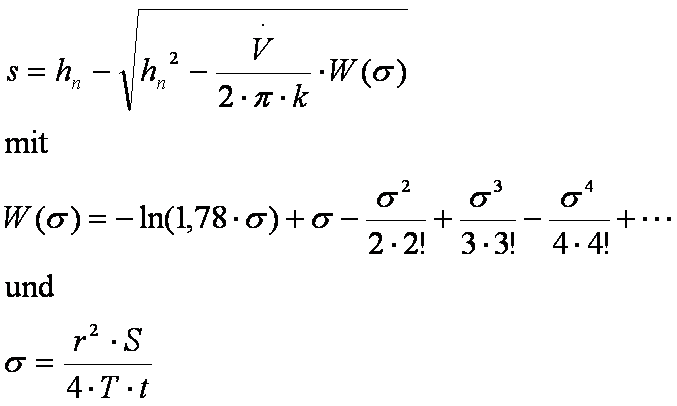
5. Berechnen Sie die Absenkung s mittels der Theis-Funktion!
6.
Benutzen Sie für die Werte S und k bzw. T
geschätzte Werte!
Diese können Sie nach Belieben ändern, um eine optimale Anpassung der
berechneten Werte an die Messwerte (à
quadratische Abweichung minimieren) zu erreichen. Als Radius kann r=5m
angesetzt werden.
Hier finden Sie die Arbeitsschritte zur Auswertung des Pumpversuches
Hier finden Sie die
Lösung zu Teil 3
Teil 4
Ausgehend von den in Teil 3 aufgestellten Tabellen sollen weitere Elemente der MS-Excel-Programmierung genutzt werden.
1. Suchen Sie aus den berechneten quadratischen Abweichungen die Werte heraus, die größer als 0,025 cm2 sind. Nutzen Sie dazu die WENN-Funktion!
2. Klassifizieren Sie die quadratischen Abweichungen in 10 Klassen und stellen Sie diese als Histogramm dar!
3. Nutzen Sie die internen Regressions-Funktionen von MS-Excel und überprüfen Sie, ob darunter welche sind, die eine bessere Anpassung erzielen, als die in Teil 3 gewählte Übertragungsfunktion!
Hier finden Sie die Arbeitsschritte zur Aufstellung von Histogrammen und Regressionsfunktionen
Hier finden Sie die Lösung zu Teil 4
Teil 5
1.
Der biochemische Sauerstoffbedarf an x Tagen
(BSBx) ist die Masse an gelöstem Sauerstoff, die von adaptierten
Mikroorganismen unter festgelegten Bedingungen (z.B. konstanter Temperatur) in
einem Zeitraum von x Tagen benötigt wird.
Berechnen Sie in einer Excel-Tabelle den maximalen biochemischen Sauerstoffbedarf
des Bodenschlammes pro Tag (BSBmax/d) in Abhängigkeit von ta
nach folgender Formel (nachFair):
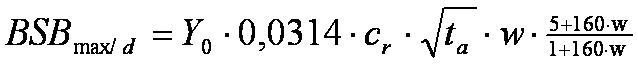
mit: 
Begriffserklärung:
|
BSBmax/d |
... |
maximaler biochemischer Sauerstoffbedarf des Bodenschlammes pro Tag |
|
Y0 |
... |
BSB5 bei 20°C (in g/kg org. Trockensubstanz) |
|
ct |
... |
Temperaturkoeffizient |
|
w |
... |
täglich abgelagerter Teil der org. Substanz (kg org. Trockensubstanz pro m²) |
|
ta |
... |
Anzahl der Tage im Jahr, an denen Bodenschlamm abgegeben wird |
2. Stellen Sie die ermittelten BSB - Werte in Abhängigkeit von ta in einem Diagramm dar!
3. Bei der Selbstreinigung von Gewässern ist die kritische Fließzeit tkr eine entscheidende Größe, da sie angibt, nach welcher Fließzeit das Minimum der Sauerstoffkonzentration in einem Gewässer erreicht wird.
Errechnen Sie die kritische Zeit in Abhängigkeit vom Sauerstoffdefizit D0 nach folgender Formel und stellen Sie die Ergebnisse grafisch dar!
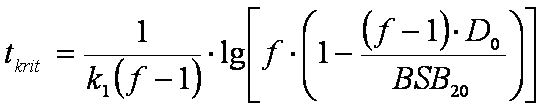
mit: 
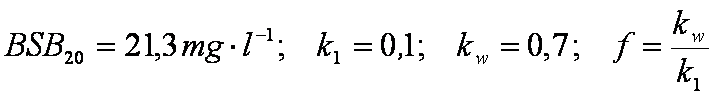
Hier finden Sie die Lösung zu Teil 5
Teil 6
Gleichungssysteme und Matrizen
1.
Stellen Sie das folgende Gleichungssystem:
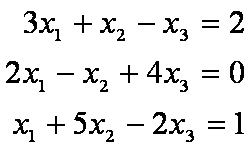(A
x = b)
in einer Excel-Arbeitsmappe als Matrix dar! Berechnen Sie
· die Determinante der Matrix
· die inverse Matrix
- nach den Methoden der Matrizenrechnung (Einzelschritte)
- mittels Funktionen von Excel
· die Lösung der Matrix
- als Produkt der inversen Matrix mit der rechten Seite
- mittels Funktionen von Excel!
2.
Berechnen Sie das Integral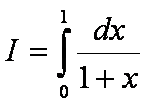 
mit Hilfe folgender numerischer Integrationsmethoden:
· Rechteckregel mit den Schrittweiten
- 0,1
- 0,01
· Trapezregel mit den Schrittweiten
- 0,1
- 0,01
Stellen Sie die Funktio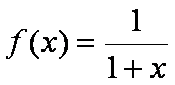n
sowie die Summen der Teilflächen der o.g. Integrationsmethoden
in einem Diagramm grafisch dar. Die grafische Darstellung soll im Wertebereich
von 0 bis 1 erfolgen.
Hier finden Sie die Lösung zu Teil 6
Teil 7
Verwenden Sie zu nachstehender Aufgabe die Excel-Tabelle unter à(GWBR-Daten-neu.xls):
1. Berechnen Sie den Grundwasserstand über NN (GW-NN = ROK – GWA (Z)!
2. Berechnen Sie den durchschnittlichen GW-Stand !
3. Klassifizieren Sie die Abweichungen vom mittleren GW–Stand in 5 Klassen und stellen Sie diese als Histogramm dar e
4. Berechnen Sie den Abstand der einzelnen Messpunkte von dem Punkt mit dem Rechtswert 5445000,0 und dem Hochwert 5706000,0. Dieser Punkt erhält den durchschnittlichen GW-Stand!
5. Stellen Sie grafisch die Abhängigkeit des Abstandes (nach Punkt 4) und den GW-Stand der einzelnen Messpunkte dar!
6. Bilden Sie zu der Abhängigkeit (nach Punkt 5) eine lineare Regressionsfunktion und stellen Sie diese mit in einem Diagramm dar!
Hier finden Sie die Lösung zu Teil 7
Teil 8
Mittels Excel und beiliegender Niederschlags-Tabelle à (Niederschlag.xls) soll folgendes berechnet und ausgewertet werden:
1. Berechnen Sie die Summe, die kumulative Summe, den Maximalwert und den Mittelwert des Niederschlages! Berechnen Sie auch das Datum des maximalen Niederschlagswertes!
2. Stellen Sie die Niederschlagsganglinie und die Summenlinie (kumulative Summe) in Abhängigkeit des Datums grafisch dar!
3. Bestimmen Sie die lineare Regressionsgerade der Summenlinie und stellen Sie diese grafisch dar!
4. Berechnen Sie eine gleitende Mittelwertbildung über sieben Tage und stellen Sie diese grafisch dar. Für die ersten und letzten sechs Tage benutzen Sie jeweils entsprechend weniger Tage zur Mittelwertbildung!
5. Bestimmen Sie die Anzahl der Regentage, die Anzahl der Tage die mehr als 0 mm, 5 mm und 10 mm Niederschlag hatten!
6.
Berechnen Sie ein Histogramm
(Häufigkeitsverteilung) zur Regenverteilung mit einer Klassenbreite von 1 mm.
Stellen Sie die Verteilung bis zu einer Niederschlagsmenge von 10 mm grafisch dar!