1.      Berechnen Sie die Absenkung für die Punkte (r) und Zeiten (t), die infolge einer Wasserförderung  im Brunnen für nachfolgende Grundwasserleiter auftritt und stellen Sie das Ergebnis grafisch dar:

        ;

;

2.      Berechnen Sie für den o.g. Grundwasserleiter die Absenkung im Punkt  alle 10 Minuten bis maximal 100 Minuten, wenn der Volumenstrom des Förderbrunnens folgender Zeitstaffelung unterliegt, und stellen Sie es grafisch dar:

3.      In einem Grundwasserleiter in der Nähe eines Flusses soll eine Baugrube abgesenkt werden. Die Mitte der Baugrube ist  vom Fluss entfernt, die Entwässerungsbrunnen . Es sind drei Brunnen parallel zum Fluss angeordnet, die jeweils  voneinander entfernt sind. Die Brunnen besitzen einen Durchmesser von  und fördern mit jeweils .

      Der Fluss besitzt eine Breite von  und eine Kolmationsschicht von  

         Der Grundwasserleiter hat folgende Eigenschaften:      

         Wird nach 10 Tagen im Zentrum der Baugrube die Zielabsenkung von  erreicht?

4.            Überprüfen Sie mittels der analytischen Lösung der Brunnenanströmung, ob der Mittelpunkt der Baugrube nach einer Zeit von sieben Tagen bei einer Förderleistung von ,  mit einer Sicherheit von  entwässert ist.

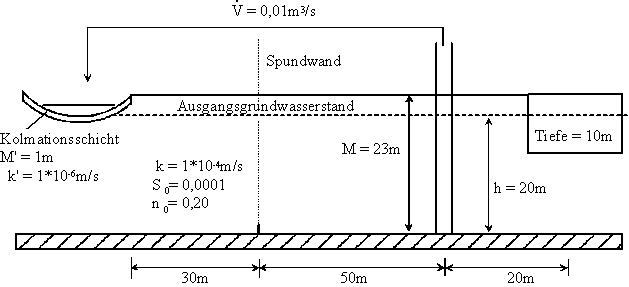
5.      Bei einem Pumpversuch in einem unendlich ausgedehnten Grundwasserleiter wurden folgende Wasserstände in Abhängigkeit von der Entfernung zum Brunnen nach einer Pumpzeit von  gemessen (siehe Skizze).

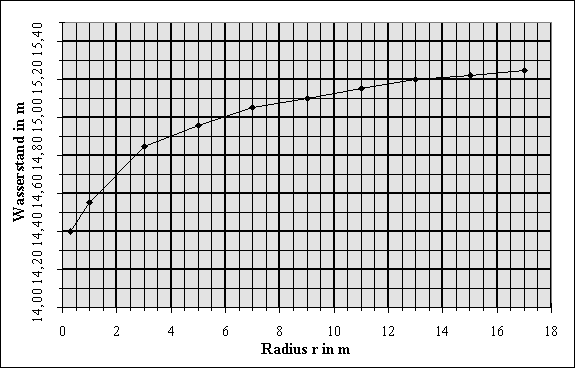
Berechnen Sie das Wasserdefizit (Volumen) des Absenkungstrichters, wenn der Grundwasserleiter folgende Kennwerte besitzt:

6.      Aus einem Brunnen, der an einem idealen Fluss ( ) liegt ( ), wird ein konstanter Volumenstrom von  gefördert. Der Brunnen hat einen Radius von . Der Grundwasserleiter ist durch folgende Parameter gekennzeichnet:

  , ,

Hinweis:           Arbeiten Sie so lange wie möglich mit allgemeinen Formelzeichen.

a.       Berechnen Sie den stationären Endzustand (Anteil der zeitlichen Funktionalität soll kleiner als 0,001 sein) für den Punkt ( ) und

b.   den Zeitpunkt, ab wann mit ihm zu rechnen ist.

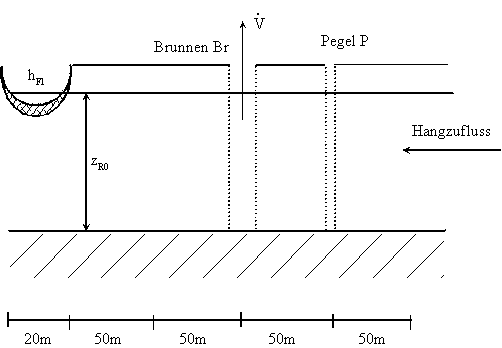
b.                                               7.   Für ein Uferfiltratswasserwerk (siehe Skizze) mit parallelem Strömungsregime ist ein Simulationssystem aufzubauen. Der Fluss soll dabei als idealisierte Randbedingung berücksichtigt werden.

c.                                                                    ,  

d.                                                          
 

Berechnen Sie für diese hydraulischen Verhältnisse den stationären Endzustand auf der Basis der analytischen Lösung der Brunnengleichung. Ermitteln Sie die Lösung

a.       mit idealisiertem Fluss

b.      unter Berücksichtigung des realen Flusses (Kolmation und Unvollkommenheit).

8.   In der Geohydraulik werden Pumpversuche zur Bestimmung der Grundwasserleiterpara­meter eingesetzt. Unter bestimmten Bedingungen kann die Absenkung nach der Formel von Theis/Jakob/Cooper

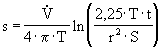
ermittelt werden.

Leiten Sie unter Verwendung dieser Formel eine Gleichung zur Bestimmung des k-Wertes für einen Ortspunkt P, der sich in einer Entfernung vom Brunnen befindet, ab. Die Bestimmung des k-Wert soll dabei auf der Verwendung der Absenkungswerte s₁ zum Zeitpunkt t₁ und s₂ zum Zeitpunkt t₂ basieren. Das Verhältnis der Messzeiten  beträgt 1:10.