kd-Baum Teachlet
Anwendung
Bei Verwendung eines 3D-Scanners werden meist aus verschiedenen Perspektiven unabhängige Ansichten (Punktwolken) eines aufzunehmenden Objektes erstellt. Dabei werden die sich überlappenden Bereiche genutzt, um die verschiedenen Punktwolken aneinander anzupassen. Nach einer groben, oft manuellen Ausrichtung, erfolgt die genaue Ausrichtung mit Hilfe des Iterative Closest Point (ICP) Algorithmus.
Bei diesem Verfahren wird jeder Punkt einer Punktwolke dem nächstliegendsten Punkt der zweiten Punktwolke zugeordnet. Um dieses Nächste-Nachbar-Problem zu lösen, muss im schlechtestem Fall der Abstand eines Punktes zu jedem anderen Punkt aus der zweiten Wolke berechnet werden. In der Praxis wird der Suchvorgang deutlich beschleunigt, indem die Punkte in der Datenstruktur eines kd-Baums gespeichert werden.
Nach dem für jeden Punkt ein nächster Nachbar aus der zweiten Punktwolke gefunden wurde, werden die Punktwolken neu ausgerichtet, so dass sich die Abstände zwischen den Punkten verringern. Dieser Vorgang wird solang wiederholt, bis ein Minimum der Summe aller Abstände gefunden wurde.
Allgemein
Ein kd-Baum ist eine Datenstruktur die es erlaubt Punkte aus dem k-dimensionalem Raum organisiert zu speichern. Jeder Knoten des Baums unterteilt dabei den Raum. Diese Unterteilung ermöglicht es Abfragen, wie die Suche des nächsten Nachbars, in deutlicher geringer Zeit zu beantworten.
Konstruktion eines homogenen 2d-Baums
Ein Knoten in einem kd-Baum entspricht einer Hyperebene die den Raum in zwei Hälften (Halbraum) trennt. Punkte eines Halbraums werden durch den entsprechenden Unterbaum repräsentiert. Um dies zu erreichen, muss die Menge an Punkten in der entsprechenden Dimension sortiert werden.
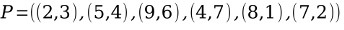
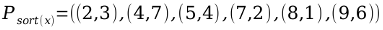
Das Medianelement dieser sortierten Menge bestimmt den neuen Knoten.
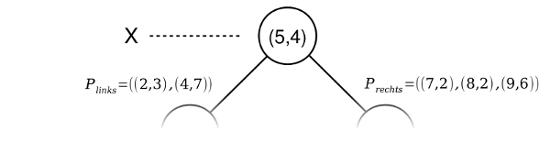
Für die Untermengen wird der Vorgang durch Rekursion mit wechselnden Hyperebenen wiederholt. Ein Ast ist konstruiert, wenn |P| = 1 und dadurch ein Blattknoten (ohne weiterführende Zweige) erstellt wird. Die Tiefe eines Knoten im Baum bestimmt entlang welcher Dimension der Raum getrennt wird (Tiefe modulo k). Für einen 2d-Baum entspricht der Wechseln dann entsprechen der Tiefe (X-Y-X-Y…) äquivalent für einen 3d-Baum (X-Y-Z-X-Y-Z…).
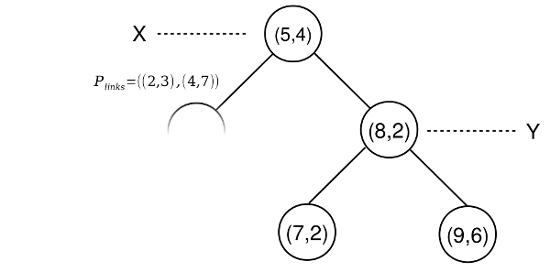
Phase I
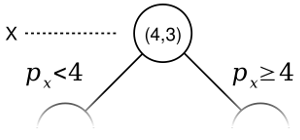
Die Suche nach dem nächsten Nachbar eines bestimmten Punktes (p) beginnt im Wurzelknoten des Baums. Während der ersten Phase der Suche erfolgt eine Tiefensuche. Das bedeutet ein Ast wird solang traversiert bis ein Blattknoten erreicht ist. An jedem Knoten wird dabei einer der beiden Zweige gewählt. Dazu werden die Koordinaten des Knotens und des gewählten Punktes verglichen, welche durch die Hyperebene getrennt werden. Ist die Koordinate des Punktes kleiner als die des Knotens wird der linke Zweig traversiert. Ist die Koordinate des Punktes größer, wird der rechte Zweig traversiert.
Phase II
In der zweiten Phase wird der aus Phase I erzeugte Pfad rückwärts aufgerufen (Rückwärtsaufruf). Für jeden nun besuchten Knoten werden zwei Aktionen durch geführt:
-
Berechnung einer Distanzkennzahl (D(p,k)) zwischen dem Punkt welcher durch den aktuellen Knoten (k) repräsentiert wird und dem gewählten Punkt (p) zu dem der nächste Nachbar gefunden werden soll. Wenn die Distanz geringer ist, als die des bisherig nächsten Knoten, wird der aktuelle Knoten zum neuen nächsten Knoten bestimmt.
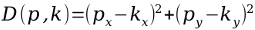
-
Falls der aktuelle Knoten weiterführende Zweige besitzt, wird überprüft, ob in dem bisher nicht besuchten Zweig eine Verbesserung möglich ist. Eine Verbesserung im Zweig ist möglich, wenn im Knoten davor (z.B. mit einer Hyperebene in der x-Dimension) folgende Bedingung gilt:
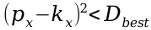
Wenn diese zu trifft, wird der komplette Algorithmus (Phase I) mit diesem Zweig erneut aufgerufen. Es kommt zur Rekursion.
Ende
Der Algorithmus terminiert, wenn der letzte Knoten (Wurzelknoten) während Phase II überprüft wurde. Der bisherig nächste Knoten ist der gesuchte nächste Nachbar.