Histogramme & Punktoperatoren
- Histogramme
- Kumulative Histogramme
- Punktoperatoren
- Beispieloperatoren
Allgemein
Ein Histogramm im Bereich der Bildverarbeitung zeigt die statistische Häufigkeit der Tonwerte eines Bildes in Form eines (diskreten) Balkendiagramms an. Es wird deshalb auch Tonwertkurve genannt. Auf der horizontalen Achse befinden sich die Tonwerte (Farb-/Helligkeitswerte). Die Höhe eines Balkens gibt an, wie häufig dieser Tonwert im Bild vorkommt. Im einfachsten Falle eines Graustufenbildes spiegelt es die Anzahl von Pixeln der Farben Schwarz (am linken Rand) bis Weiß (am rechten Rand) wieder.
Die Anzahl der Pixel mit dem Tonwert g wird durch die Funktion h(g) beschrieben. Die Tonwerte liegen dabei meist im Intervall [0, 255] vor, da mit 8 Bit pro Kanal genau 2^8=256 verschiedene Werte abgebildet werden können.
Anhand eines Histogramms kann man die Tonwertverteilung und somit die korrekte Belichtung (Unter-/Überbelichtung), den Kontrast und andere visuelle Attribute des Ausgangsbildes abschätzen. Es gibt keine Möglichkeit das Originalbild aus einem Histogramm zu rekonstruieren, da jede unterschiedliche Anordnung von Pixelwerten genau das selbe Histogram aufweist.
Farbbilder
Auch für Farbbilder lassen sich Histogramme erstellen. Eine Möglichkeit besteht darin, für jeden Kanal ein einzelnes Histogramm zu erstellen. Diese können optional auch in ein Histogramm überblendet werden. Auch für RGB Farbbilder lässt sich eine Pixelhelligkeit berechnen. Durch die Farbraumtransformation von RGB nach YCbCr erhält man die Pixelhelligkeit Y, welche im CIE-Normvalenzsystem vorliegt. Die Berechnungsvorschrift lautet dann: Y = 0.299 * R + 0.587 * G + 0.114 * B.
Histogrammerstellung
Zur Histogrammerstellung müssen die Tonwerte zuerst in Klassen unterteilt werden. Standardmäßig besitzt jeder Tonwert seine eigene Klasse. Nun muss über alle Pixel im Bild iteriert und deren Klasse bestimmt werden, um die absoluten Klassenhäufigkeiten aufzusummieren. Abschießend wird für jede Klasse ein Balken in der Höhe der Häufigkeit gezeichnet.
Beispiele
Hier können für eigene Bilder als auch verschiedene Testbilder Histogramme für die Helligkeit, kombinierte und einzelne RGB-Kanäle generiert werden:

Allgemein
Das kumulative Histogramm stellt eine monoton steigende Folge von Werten im Bereich [0,K] dar, wobei K der Anzahl der Pixel im Bild entspricht.
Dieses Histogramm wird berechnet, indem jedem Grauwert g die Summe aller Häufigkeiten H der Grauwerte 0 bis g zugeordnet wird:
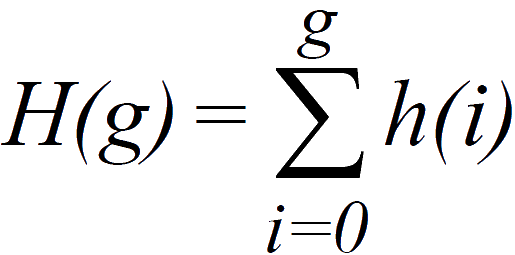
Sind alle Tonwerte gleich Häufig vorhanden, so ergibt sich eine monoton steigende Gerade.
Beispiele
Hier können für eigene Bilder als auch verschiedene Testbilder Histogramme und die dazugehörigen kumulativen Histogramme für die Helligkeit, kombinierte und einzelne RGB-Kanäle generiert werden:

Allgemein
Als Punktoperatoren bezeichnet man Bildverarbeitungsoperationen, welche sich dadurch auszeichnen, dass ein neuer Farb- oder Grauwert eines Pixels allein in Abhängigkeit von seinem eigenen bisherigen Farb- oder Grauwert und seiner eigenen bisherigen Position im Bild berechnet wird, ohne dabei von seiner Nachbarschaft abzuhängen.
Neben den Punktoperatoren, die jedes Pixel eines Bildes einzeln transformieren, gibt es mit den lokalen Operatoren und den globalen Operatoren zwei weitere Klassen von Bildverarbeitungsoperationen. Lokale Operatoren berechnen einen neuen Farb- oder Grauwert eines Pixels immer auf Basis einer Nachbarschaft oder einer örtlich begrenzten Region um das Pixel. Hier seien als Beispiele Rangordnungsoperatoren oder morphologische Operatoren genannt. Globale Operatoren betrachten für die Transformation eines jeden Pixels immer das gesamte Bild, was beispielsweise bei der Fourier-Transformation der Fall ist.
Definition
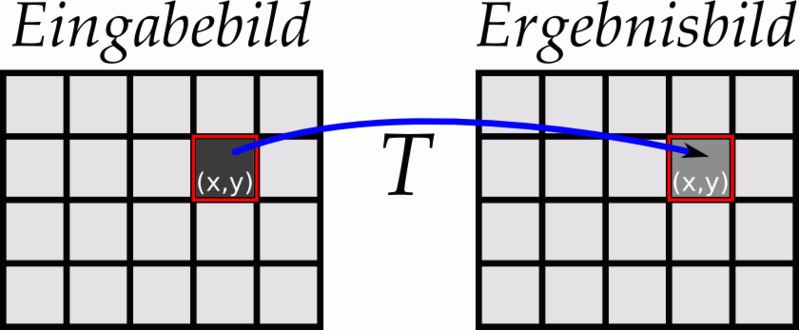
Ein Punktoperator T ordnet einem Eingabebild f durch Transformation der Farbwerte der einzelnen Pixel ein Ergebnisbild f* zu. Der Farbwert f(x,y) eines Pixels (x,y) wird dabei nur in Abhängigkeit vom Farbwert selbst und eventuell von der Position des Pixels im Bild modifiziert. Ist die Transformation von der Position des Pixels im Bild abhängig, so heißt sie inhomogen:
![]()
Ist die Transformation unabhängig von der Position des Pixels im Bild, wird sie als homogen bezeichnet:
![]()
Im Allgemeinen sind Punktoperatoren nicht umkehrbar. In manchen Fällen wie zum Beispiel bei der Invertierung kann dies trotzdem möglich sein.
Anwendung
Bei Verwendung von diskreten Farbwerten [0,n] kann eine homogene Transformation durch das Nachschlagen in einer Look-up-Tabelle der Größe n implementiert werden. Bei 8 Bit Pro Farbwert sind dies nur 2^8 = 256 vorzuberechnende Einträge. Bei kontinuierlichen Farbwerten oder inhomogenen Punktoperatoren ist dies inpraktikabel und die Transformation muss für jedes Pixel neu berechnet werden, da die entstehende Tabelle durch die unendlich vielen möglichen Farbwerte praktisch nicht mehr berechnet werden kann.
Transformationskennlinie
Homogene Punktoperatoren können durch eine Transformationskennline (Gradationskurve) beschrieben werden. Sie zeigt, welche Farbwerte des Ausgangsbildes zu welchen Farbwerten im Ergebnisbild transformiert werden. Wertebereich als auch Definitionsbereich sind somit die Farbwerte des Bildes. Zum besseren Verständnis des Abbildungsverhaltens eines Punktoperators können Histogram und Transformationskennlinie überlagert werden. Dies ist im folgenden anhand einer Logarithmustransformation illustriert.


© 2014 Johannes Pietrzyk, Benjamin Worpitz