Simulationsprogramm ASM

1.      Simulieren und stellen Sie grafisch die Absenkung für die gegebenen Punkte (r) und für folgende Zeiten (t) infolge einer Wasserförderung  im Brunnen für folgenden Grundwasserleiter dar:

k = 1·10-3 m/s; M = 10 m; S = 0.001; a = S/T = 0.1 s/m2; r0 = 0.25 m; ;

hn = 16 m;

 

r = 5 m; 10 m; 20 m; 50 m

t = 1 min; 2 min; 5 min; 10 min; 20 min; 30 min; 45 min; 60 min; 90 min; 120 min

 

2.      Simulieren und stellen Sie für den o.g. Grundwasserleiter die Absenkung im Punkt (r = 10 m) alle 10 Minuten bis maximal 100 Minuten grafisch dar, wenn der Volumenstrom des Förderbrunnens folgender Zeitstaffelung unterliegt:

 

Volumenstrom / [m3/s]

0,005

0,01

0,015

0,02

0,025

0,03

0,000

Förderbeginn / [min]

0

10

20

30

40

50

60

 

3.      In einem Grundwasserleiter in der Nähe eines Flusses soll eine Baugrube abgesenkt werden. Die Mitte der Baugrube ist 100 m vom Fluss entfernt, die Entwässerungsbrunnen 80 m. Es sind drei Brunnen parallel zum Fluss angeordnet, die jeweils 25 m voneinander entfernt sind. Die Brunnen besitzen einen Durchmesser von r0 = 0,3 m und fördern mit jeweils 0,015 m3/s.

Der Fluss besitzt eine Breite von B = 20 m und eine Kolmationsschicht von

k’ = 3·10-6 m/s; M’ = 1 m.

Der Grundwasserleiter hat folgende Eigenschaften: k = 5·10-4 m/s; n0 = 0,20;

hn = 15 m; M = 20 m.

Wird nach 10 Tagen im Zentrum der Baugrube die Zielabsenkung von 2,5 m erreicht?

 

4.      Überprüfen Sie mittels des Simulationsprogrammes ASM, ob der Mittelpunkt der Baugrube nach einer Zeit von sieben Tagen bei einer Förderleistung von  = 0,01 m3/s, r0=0,30 m mit einer Sicherheit von 0,5 m entwässert wird.


 


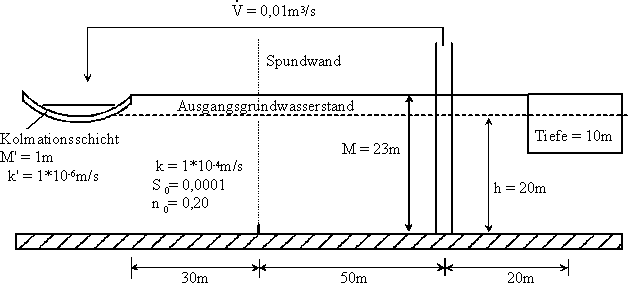
Aus einem Brunnen, der an einem idealen Fluss liegt (Br(100m, 500m)) wird ein konstanter Volumenstrom von 25 l/s gefördert. Der Brunnen hat einen Radius von r0 = 0,35 m. Der Grundwasserleiter ist durch folgende Parameter gekennzeichnet: hn = 15 m, M = 17 m, k = 1 10-3 m/s, S0 = 0,0002, n0 = 0,25.

Simulieren Sie den stationären Endzustand (Anteil der zeitlichen Funktionalität soll kleiner als 0.01 sein) für den Punkt (P(600m, 200m)) und ermitteln Sie den Zeitpunkt ab wann mit ihm zu rechnen ist.

 

5.        Simulieren Sie folgende eindimensionalen Grundwasserströmungen:

a.             Simulieren Sie mittels einer eindimensionalen stationären Grabenströmung die Lage der freien Oberfläche in Abhängigkeit von x und ermitteln Sie den Abfluss aus dem Oberwasser und den Zufluss zum Unterwasser. Verwenden Sie dabei fünf Quantisierungselemente.

 

 


 

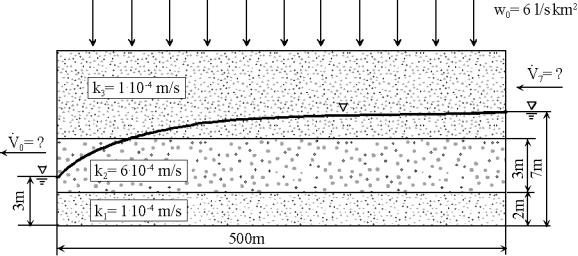
k3 = 1 10-4 m/s
 

k1 = 1 10-4 m/s
 
 

 

 


b.            Simulieren Sie mittels einer eindimensionalen instationären Grabenströmung die Lage der freien Oberfläche in Abhängigkeit von x und der Zeit t.

 

 

 


 

 


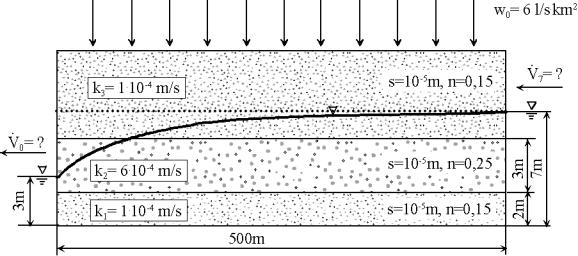
7.         In einem Grundwasserleiter soll ein Tunnel (U-Bahn) parallel zu einem Fluss eingebaut werden. Simulieren Sie, zu welchen Grundwasserstandsänderungen es für den stationären Fall durch diesen Einbau kommt. Wählen Sie dazu ein geeignetes grobes Quantisierungsschema.

 

 

 


 

 


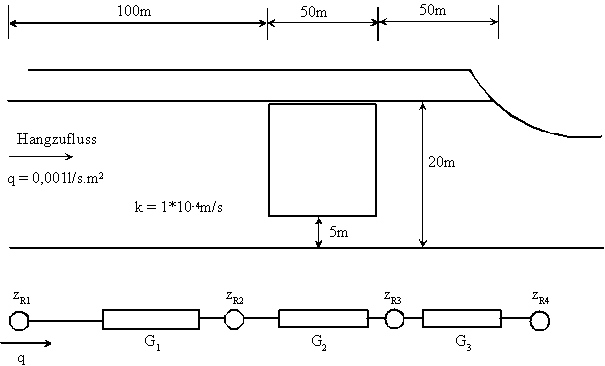
8.         In einer Flussniederung soll mittels eines Deichbauwerkes das Poldergebiet vor Hochwasser geschützt werden. (entsprechend vereinfachtem Schema)

Ermitteln Sie die Zeit, nach welcher sich ein stationäres Strömungsregime eingestellt hat, wenn das Hochwasser über lange Zeit 5 m über normal steht.

Wieviel Wasser fließt pro Meter Deichlänge in das Poldergebiet.

Deich:                             k = 10-4 m/s, n0 = 0,15, S0 = 0,002;


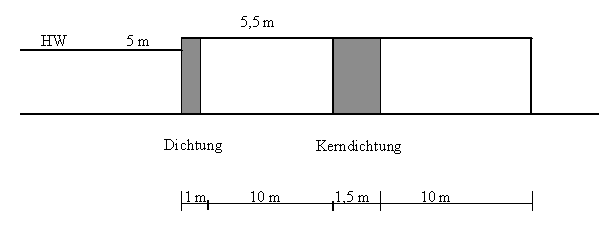
Dichtungsmaterial:           k = 10-5 m/s; n0 = 0,05; S0 = 0,001

 

 

5,5 m
 

0 m
 
 

 


9.         Modellieren Sie mittels des Programmsystems ASM folgenden horizontalen Grundwasserleiter, der rechts und links von zwei vollkommen ausgebauten Vorflutern mit einer Wasserhöhe von 50 m begrenzt wird. Der Grundwasserleiter besitzt eine Mächtigkeit von 20 m, eine Transmissibilität von T = 0,01 m2/s, einen Speicherkoeffizient von S = 0,001 und eine Porosität von 0,1. In der Mitte des Modellgebietes liegt ein Brunnen mit einer Förderleistung von .

 

a.            Simulieren Sie die Wasserstandsverteilung (Isohypsenplan) nach einer Förderzeit des Brun­nens von einem Tag.

b.           Stellen Sie grafisch die Wasserstandsganglinien am Brunnen und jeweils 200 m (parallel und senkrecht zum Vorfluter) entfernt dar.

c.            Berechnen Sie die Wasserbilanz für das Modellgebiet nach eintägiger Förderung, sowie den Zufluss von dem linken Vorfluter.

d.            Untersuchen Sie zu dem hydraulischen System der Aufgabe 3 den Einfluss der Orts- und Zeitquantisierungsschrittweiten und den der Lösungsverfahren. Stellen Sie dazu vor allem die Hydroisohypsen nach einem Tag dar und vergleichen Sie diese.

 

Hier finden Sie die Lösung für die Aufgabe von Teil 1.