1. Berechnen
Sie mittels der Methode der Übertragungsglieder bei einem Volumenstrom von 
die Absenkungskurve für eine Förderleistung
von 
,
wenn der Pumpversuch folgende Werte lieferte, und stellen Sie grafisch dar:
|
Zeit
|
320 |
426 |
564 |
743 |
976 |
1279 |
1673 |
2185 |
2850 |
3715 |
4839 |
6302 |
8202 |
10000 |
|
Absenkung
|
0,63 |
0,69 |
0,73 |
0,77 |
0,81 |
0,85 |
0,88 |
0,92 |
0,96 |
0,99 |
1,03 |
1,06 |
1,10 |
1,14 |
2. Bestimmen Sie für folgende gefundene Messreihe, die durch Einspeisung einer Funktion entstanden ist, die Übertragungsfunktion einschl. der Parameter.
|
t |
|
|
t |
s |
|
0 |
0 |
|
0 |
0 |
|
1 |
0,1 |
|
1 |
0,01 |
|
2 |
0,1 |
|
2 |
0,08 |
|
4 |
0,1 |
|
4 |
0,13 |
|
8 |
0,1 |
|
8 |
0,19 |
|
15 |
0,1 |
|
15 |
0,25 |
3. Bei
einem Pumpversuch ist für einen Grundwasserstandort folgende Abhängigkeit
zwischen Förderstrom 
und Grundwasserabsenkung s gefunden worden:
|
|
s |
t |
|
0 |
0 |
-1 |
|
0,05 |
0 |
0 |
|
0,05 |
3 |
1 |
|
0,05 |
8 |
2 |
|
0,05 |
20 |
4 |
|
0,05 |
30 |
10 |
|
0,05 |
35 |
20 |
|
0,05 |
37 |
40 |
|
0,05 |
38 |
100 |
Berechnen
Sie den Verlauf der Absenkung bei einer Förderrate von 
und stellen Sie grafisch dar. Verwenden Sie
dazu die Methode der Übertragungsfunktionen.
4. Bei
einem Gütepumpversuch wurden für zwei unterschiedliche Standorte P1
und P2, die sich in einer Entfernung vom Infiltrationsbrunnen von 
und 
folgende Konzentrationswerte C gefunden. Am
Infiltrationsbrunnen wird eine dauerhafte Konzentration von 
beigegeben.
|
t |
0,5 |
1,0 |
1,5 |
2,0 |
2,5 |
3,0 |
3,5 |
4,0 |
4,5 |
5,0 |
5,5 |
|
Cr1 |
2,40 |
2,70 |
3,05 |
3,55 |
4,0 |
6,50 |
7,95 |
8,70 |
9,10 |
9,20 |
9,25 |
|
Cr2 |
2,40 |
2,70 |
3,04 |
3,32 |
3,57 |
3,81 |
4,01 |
4,20 |
4,37 |
4,53 |
4,67 |
Berechnen Sie die Übertragungsfunktionen für diese Systeme.
5. Bei
einem Tracerversuch wird an dem Brunnen 1 eine Stoffkonzentration von 
NaCl 5 min lang in den Boden infiltriert.
Berechnen und stellen Sie grafisch den Verlauf einer möglichen
Schadstoffausbreitung dar, wenn durch eine Havarie 1000 kg Schadstoffe in den
Boden gelangt wären.
|
t |
24 |
30 |
35 |
40 |
42 |
50 |
60 |
70 |
80 |
90 |
100 |
120 |
|
C |
0 |
2,0 |
7,0 |
9,7 |
9,8 |
7,5 |
5,0 |
3,5 |
1,5 |
0,5 |
0,3 |
0 |
7. Prognostizieren Sie den Temperaturverlauf der Fassung unter Verwendung des Faltungsintegrals, wenn folgende Messwerte bekannt sind.
|
dFluss
|
14,2 |
16,0 |
17,7 |
19,4 |
17,2 |
16,0 |
17,6 |
18,6 |
14,8 |
12,0 |
13,7 |
|
dFassung
gemessen
|
8,5 |
10,0 |
11,4 |
14,0 |
14,1 |
14,7 |
15,4 |
15,8 |
15,6 |
14,9 |
14,1 |
|
dFassung
prognostiziert |
|
|
|
|
|
|
|
|
|
|
|
|
Zeit |
0 |
15 |
30 |
45 |
60 |
75 |
90 |
105 |
120 |
135 |
150 |
Berechnen Sie den Temperaturverlauf ab dem sechsten Zeitschritt unter Verwendung von jeweils drei Gleichungen des Faltungsintegrals. Vergleichen Sie die berechneten Temperaturen in der Fassung mit den gemessenen und korrigieren Sie die Gewichtsfunktionsanteile unter Berücksichtigung der gemessenen Werte.
8. Bei einem Säulen-Durchlaufversuch wurde folgende Impulsantwortfunktion auf einen Konzentrationsstoß von 30 mg/l eines Schadstoffes gemessen.
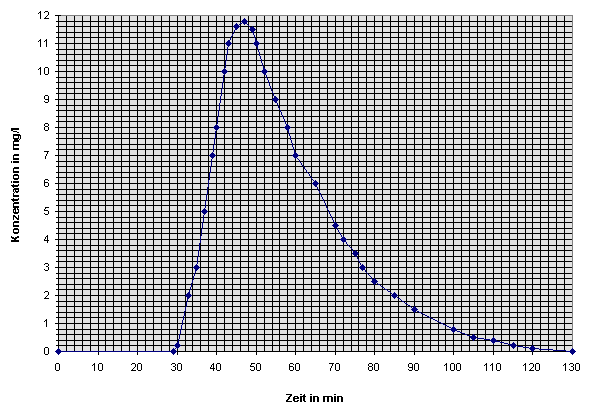
a) Bestimmen Sie zu diesen Messwerten die Gewichtsfunktion und die Übertragungsfunktion.
b) Prognostizieren Sie die Konzentration nach 160 min, wenn die Eingangskonzentration folgenden zeitlichen Verlauf hat.
|
Zeit |
0 |
20 |
40 |
60 |
80 |
100 |
120 |
140 |
|
C |
30 |
50 |
80 |
60 |
100 |
50 |
10 |
0 |
Hier finden Sie die Lösung für die Aufgabe von Teil 1-6.
Hier finden Sie die Lösung für die Aufgabe von Teil 7.